Efforts to understand the meanings of the temperature and entropy of a black hole are leading to the conclusion that spacetime must be discrete and elucidating its structure. Entropy outside of a black hole's horizon is a measure of missing information. But the entropy of a black hole is related to the area of the horizon, which is a geometric quantity. To reconcile the difference between the two types of entropy, it seems that spacetime must have an atomic structure. The relationship between entropy and area also indicates that if we understand the atomic structure of geometry then it will be clear why the area of the horizon specifies the amount of information hidden behind it.

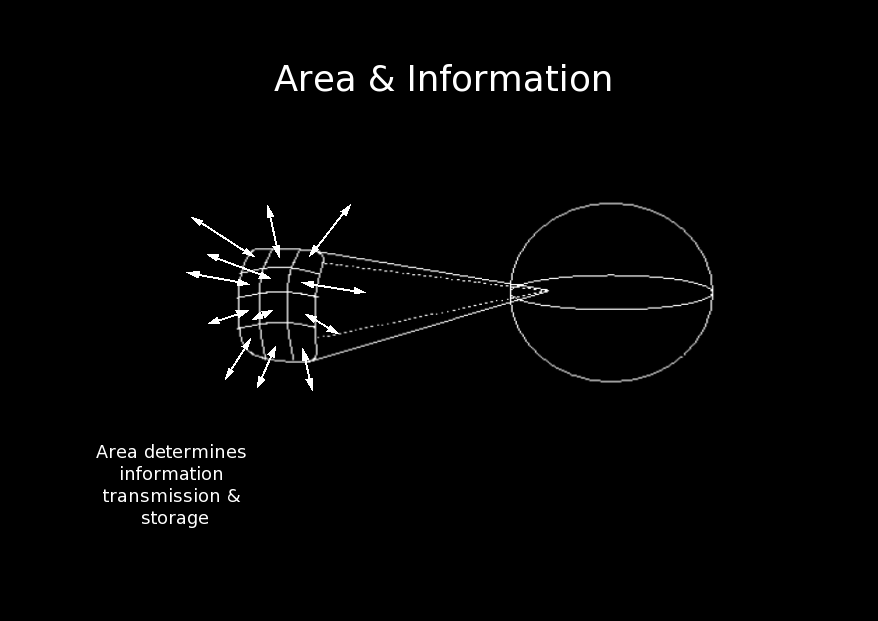
Processes structure spacetime by transmitting information from the past to the future. Surfaces act as conduits for information. Therefore, it seems natural that the area of a horizon should be related to its capacity to transmit information. But it seems more reasonable that the capacity of a region to trap information would be proportional to the volume of the region rather than the area of the region's boundary. If spacetime was continuous, than every region could contain an infinite amount of information. However, since the amount of information that can be stored in a region is proportional to the area of its boundary, each region can only store a finite amount of information and must therefore be discrete.

There are on the order of 10⁶⁶ bits of information per cm² of horizon that can be stored in a region. This limitation is called Bekenstein's bound. Notice that any region can be a hidden region for an appropriately accelerating observer. This means that these conclusions apply to all of spacetime.